|
| |
|
Design of a Long Overland Conveyor
with Tight Horizontal Curves
|
J.L. Page, R.S. Hamilton,
G.G. Shortt and P. Staples, South Africa
Courtesy : Trans Tech Publications - Bulk Solids Handling Journal
Summary
This paper describes the design, construction, commissioning and testing of a 1,000 t/h capacity,
3.2 km long overland belt conveyor that incorporates two 1,350 m radius horizontal curves, taking the
path of the conveyor through an angle of 950. The conveyor forms part of Amcoal's new Landau Colliery
The static design and dynamic simulations were carried out within the Anglo American Corporation. This
was followed, at the University of the Witwatersrand, by a series of iterative studies of the effects
of a variable speed electrical drive. The design was audited by Bateman Materials Handling, using
proprietary software.
The main features are highlighted, i.e. the use of differential-flow fluid couplings to control the
belt start-up, the inclusion of additional drive inertia to extend and control the belt shut-down,
and the idler banking in the horizontal curves.
After successful commissioning and testing, the conveyor system received a 1993 Projects and Systems
Award from the South African Institution of Mechanical Engineers.
1. Introduction
Amcoal's Landau Colliery is situated 85 km due east of Pretoria and 120 km north-east of Johannesburg.
The colliery forms part of South African Coal Estates which also operates the Rapid Loading Terminal
(RLT). Coal is railed from the RLT to the Richards Bay Coal Terminal for export.
In 1990, Amcoal embarked on feasibility studies to source coal to meet its increased share of
export capacity at the Richards Bay Coal Terminal and also to replace the old Landau No. 3 reserves
which would be depleted in 1993. These studies led to the development of the new Landau Colliery,
exploiting the Kromdraai reserves and processing the coal through a new washing plant built on the
site of the old Navigation washing plants.
As part of the new Landau development, a 3.2 km overland belt conveyor was required to feed
export coal from the new Navigation Plant to the RLT. Property ownership boundaries dictated a tight
curved route. The conveyor has a capacity of 1,000 t/h. It incorporates two 1,350 m radius horizontal
curves, taking its path through an angle of 95°.
This paper describes the design, construction, commissioning and testing of the overland conveyor.
The static design and dynamic simulations were carried out within the Mechanical Engineering
Department of the Anglo American Corporation of South Africa Limited (AAC), assisted by the
University of the Witwatersrand (Department of Electrical Engineering) in examining the suitability
of a variable speed electrical drive. Bateman Materials Handling Limited audited the design,
using proprietary software, and contributed during commissioning.
The main features are highlighted, i.e. the use of differential-flow fluid couplings to control
the belt start-up, the inclusion of additional drive inertia to extend and control the belt
shut-down, and the idler banking in the horizontal curves.
2. Conveyor Requirements
2.1 Capacity and Belt Specification
The material to be conveyed was coal of -32 mm size and a density of 0.85 t/m³.
The design capacity was set at 1,000 t/h for the initial condition, with the requirement that the
system be considered for a capacity of 1,500 t/h for the future condition.
The belt width was fixed at 1,050 mm, in order to be compatible with the existing overland conveyor
systems from the neighboring Kleinkopje Colliery. This fixed the belt class as well (ST 850), since
it was envisaged that a single source of spares could be utilized. This choice also allowed quick
access to either mine in the case the need arose for emergency spares.
2.2 Restricted Route
Several conveyor routes were investigated. The most obvious route was the direct one. However, this
entailed crossing ground belonging to another mining group. The ground had been undermined, leaving
irregular pillars. The route also meant crossing an active vlei. All this made the direct route
less attractive.
The selected route was determined by economic factors. To exclude the purchase of extra land,
including the mining rights, the conveyor was required to follow a disused Amcoal railway servitude
curving down towards the RLT. The chosen route implied that the conveyor would be required to
negotiate two very tight horizontal curves and cross the national road from Ogies to Witbank, as
well as a double railway line running alongside the road. Further down the route, there were two
minor access roads to negotiate.
Fig. 1 shows a plan of the conveyor route. The horizontal tail curve and head curve radii were
1,330 m and 1,350 m respectively, and the overall included angle was 950. This meant that the
horizontal curve radii were amongst the smallest in the world, and the included angle one of the
largest, for this type of conveyor.

Fig. 1: Plan of conveyor route
The original layout considered elevating the conveyor over the major road and rail crossing. The
7 m elevated gantry would have had to span approximately 100 m. The cost of the steelwork, with
the danger of wash-down and spillage onto the road or the rail eventually resulted in the decision
being taken to cross the road and rail underground. The crossing itself is also in one of the
horizontal curves and this would have made the elevated option more difficult and costly than would
normally be the case, given that the gantries would have had concrete floors.
At the two minor roads, the conveyor crossings were both achieved by means of concrete culvert and
ramps on each side.
The coal had to be discharged into a 6,000 t holding silo, at 49 m above ground, before being
conveyed across another road into the RLT complex. To allow for a second feed to another holding
silo in the future, it was decided to stop the overland conveyor short and transfer onto a second
conveyor to the silo.
The conveyor therefore has an overall net fall of 13 m from the tail to the head. The lowest point
on the conveyor carrying strand occurs at the approach to the head end. This point is at -21 m with
respect to the tail.
The drive pulleys are located on the ground behind the head pulley.
3. Design Procedure
3.1 Static Design
Based on the above conveyor requirements, the initial static design was undertaken according to
the usual AAC design procedure [1] and produced the following results:
| Belt Width |
1,050 mm |
| Belt Specification |
ST 850 steelcord |
| Belt Speed |
3,57 m/s |
Drive Configuration
|
Induction motors
and fluid
couplings: 2 stage
primary 1 stage
secondary |
| Start-up Procedure |
Soft start |
Tension Distribution
|
T1 = 107kN
"tight" sideT2 = 14kN
"slack" side Te = 93kN
effective tension Te = 8kN
minimum tension |
| Take-up |
Gravity |
Power requirements
|
Empty belt
170 kWFully loaded belt
331 kW |
| Motor selection |
3 x 132 kW |
| Reducer ratio |
25.6:1 (nominal) |
| Pulley diameters
|
Head 800 mm Drive 1,250 mm High tension
800 mm Low tension
630 mm |
| Idler pitch
|
Carry: 1.2 m Return:
in curve 3 m
Out of curve 6 m. |
3.2 Dynamic Simulation
The use of static design techniques alone is adequate in the case of short plant conveyors where
belt flexibility does not significantly affect the behavior of the belt during starting and
stopping. However, in the case of long overland conveyors, where tension waves generated at drive
and braking pulleys take a considerable amount of time to propagate along the length of the flexible
belt, more detailed dynamic analysis is required to ensure acceptable system behavior under start-up
and shut-down conditions. Elements of system behavior that cannot be adequately predicted using
static analysis alone include peak belt tensions, displacement of gravity take-ups, belt slippage
over drive pulleys and forces generated in holdback devices.
Dynamic analysis of the overland conveyor was carried out within AAC on a 386-PC using ACSL
(Advanced Continuous Simulation Language). This is a general purpose language, based on FORTRAN,
designed to help the engineer to mathematically model and analyze the behavior of continuous-time
systems. In ACSL, the system to be simulated is defined using linear or nonlinear differential
equations. These are then integrated numerically over short time steps to produce time histories of
system response. ACSL has been used in the Mechanical Engineering Department since 1989 to model
various systems, mostly winder related.
The model of the conveyor consisted three main elements: (1) the mechanical subsystem comprising the
belt, idlers, take-up, pulleys, reducer and later the fly-wheels; (2) the drain-type fluid couplings
and their associated oil-flow regulating system; and (3) the induction motors.
3.2.1 Mechanical Subsystem
In modeling the belt, only axial motion was considered. Although lateral motion of the belt in the
tight horizontal curves was an important design consideration, the strong damping of
lateral motion allowed adequate predictions to be made using static equilibrium calculations based
on dynamically simulated belt tensions.
The mass of the belt; idlers and load material was represented by 32 lumped masses evenly spaced
along each of the carrying and return strands (as shown in Fig. 2). The masses were connected by
springs which were linear under tension but exerted no compressive force. Motion of the masses was
resisted by Coulomb friction elements with friction constants set to correspond to the composite
friction factor used in the AAC static analysis. Since the steel cords dominate the elastic
behavior of the belt chosen for the conveyor, the more complex viscoelastic behavior of the rubber
which needs to be modeled when using more flexible belt constructions), was ignored. Nonlinear
stiffness effects introduced by sagging of the belt between the idlers was also considered to be a
secondary effect and was ignored. Due to the high stiffness of the short lengths of belt connecting the
head pulley and the two drive-pulleys, these three inertias were treated as a single node with
rigid connections. Intermediate tensions and the tension ratios across the drive pulleys were
calculated using the principle of dynamic equilibrium.

Fig. 2: Conveyor Mechanical Model
The vertical topography of the conveyor was used in the model to calculate, for each belt node, the
component of belt and load weight acting axially to the belt.
The number of nodes in the carrying and return strands can be varied. In this way, a sensible
balance between accuracy and computation speed can be determined. It was found that, contrary to
expectations, as few as 10 elements in each strand are sufficient to predict the primary dynamic
effects during start-up and shut-down.
3.2.2 Modeling of Fluid Couplings
The fluid coupling transmits torque generated by the induction motor to the drive pulley via the
reducer. The amount of torque transmitted depends primarily on (1) the volume of oil in the coupling
and (2) the speed of the output shaft relative to that of the input shaft (referred to as slip).
Characteristic torque-slip curves are supplied by coupling manufacturers. The curves for the Voith
487 TPE coupling (see Fig. 3) were defined in the ACSL model as a matrix of torque values. During a
simulation, torque was calculated by two dimensional interpolation using the input and output shaft
speeds and the volume of oil in the coupling, all of which were state variables of the system.
The rate Qout at which oil drains from a Voith 487 TPE coupling when rotating at rated
speed can be approximated by the following nonlinear equation supplied by the coupling manufacturer.

Fig. 3: Characteristic torque-slip curves for fluid coupling
(for various
oil volumes in litres)
= 0.0475 √F(15-0.25f) + 0.317
where: Qout is in litres/sec
F is the volume of oil in the coupling in litres.
Oil flow into the coupling is controlled by a solenoid valve in an on-off fashion (Qin is
either 1.0 l/s or zero).
The volume of oil F(t) in the coupling at any time was obtained in the ACSL program by integrating
the nett flow rate of oil, i.e.
F(t) = t∫0 [Qin(t) - Qout
(F,t)]dt
3.2.3 modeling of Induction Motor
The induction motors were represented in the ACSL model by the equation of the non-transient torque
curve given below (Fig. 4). However, since fluid is only pumped into the couplings once the motors
are running in the steep operating region of the curve, motor speed variation has minimal effect on
the dynamics of the conveyor. A constant speed representation of the motors would be adequate for
most start-up and shut-down simulations.
Fig. 4: Characteristic of a 132 kW induction motor
3.3 Changes to Solve Dynamic Problems
Arising from the dynamic analysis, a number of changes were made to aspects of the conveyor
configuration to solve problems which arose.
3.3.1 Increased Take-Up Tension
The preliminary selection of take-up tension (14 kN) was inadequate to overcome belt slip on
start-up, as evidenced by comparing the tension ratios (T1/T2) across the drive pulleys with the
critical value of 3.2 (see Fig. 5). Hence the take-up tension was increased to a minimum of 20 kN.
Fig. 5: Tension ratios across drive pulleys
3.3.2 Extended Start-Up Time
The static design calculated the conveyor start-up time to be 38 seconds. On simulating the
start-up, high peak tensions were produced. These high tensions were reduced by extending the
start-up time to 120 seconds (Fig. 6).
Fig. 6a: Belt tensions (start-up)
3.3.3 Control of Maximum Torque During Start-Up
To maintain the start-up torques below the limit of the electric motors, and to achieve the
extended start-up time, a maximum start-up torque limit was imposed and used to control the power
applied by the motors. This was achieved in practice by controlling the oil flow into the fluid
couplings using an on-off solenoid valve. Fig. 7 shows the "saw-tooth" torque profile during
acceleration of the belt to full speed. The very long accelerating time, however, required the
installation of bigger (160 kW) motors to minimise the thermal effects of the extended
accelerating period under full load.
Fig. 7: Primary drive fluid coupling torque
3.3.4 Control of Shut-Down Using Flywheels
On shut-down it was found that theoretically "negative" tensions were developing in the
carry strand (Fig. 8). To solve this, the take-up tension was further increased to 30 kN and
inertia, in the form of a flywheel, was added to each drive unit. The alternative of a tail
brake was rejected as an inferior solution to flywheels. The improved shut-down tension
behavior is shown in Fig. 9.
Fig. 8: Belt tensions (shut-down)
Fig. 9: Belt tensions with flywheels (shut-down)
3.4. Increased Capacity
The future capacity of 1,500 t/h was allowed for in the static design and the dynamic analyses. It
was found that the following aspects would have to be changed, as indicated in Table 1.
To allow for these changes, the drive baseframes were manufactured for the future condition, with
adapters to suit the smaller components. The take-up tower and counterweight were designed for the
maximum load (18,000 kg). The flywheel was designed to allow for additional annular rings to be
bolted onto the primary disc to increase the inertia. The structure was designed to accommodate the
maximum expected tensions.
| |
1,000 t/h |
1,500 t/h |
| Belt Speed |
3.57 m/s |
5.30 m/s |
Tension Distributor
|
T1
T2
Te
Ts |
123 kN
30 kN
93 kN
8 kN |
134 kN
40 kN
94 kN
8 kN |
| Power Requirements - full belt |
331 kW |
500 kW |
| Motor Selection |
3 x 160 kW |
3 x 220 kW |
| Fluid coupling selection |
Voith 487TPE |
Voith 562TPE |
| Reducer ratio |
26.6/1 |
17.9/1 |
| Take up mass |
13,500 kg |
18,000 kg |
| Inertia |
40 kg/m² |
80 kg/m² |
| Drive pulley diameter |
1,250 mm |
1,250 mm |
Table 1: Comparison of parameters for the increased capacity
4. Choice of Drive System
4.1 Fluid coupling
Fluid couplings are well known in mechanical drive systems to accelerate loads with high inertia.
Differential-flow (acceleration control) couplings were chosen for this application due to their
simplicity, cost effectiveness, ability to control the belt start-up to any desired format and
the facility to run the conveyor at belt inspection speed without the use of a separate pony drive.
Each coupling consists of a normal traction coupling surrounded by an oil-tight enclosure
(Fig. 10). The rotor is fitted with orifices in the periphery. The coupling is initially
empty of oil. The drive motor is started under no load. Oil is then pumped from a separate reservoir,
through a solenoid valve, to the rotor. As the coupling fills with oil, torque is transmitted to
the output stator which steadily accelerates. Oil continuously drains from the coupling, but the
coupling fill is determined by the higher flow entering the coupling (hence the term
"differential-flow").
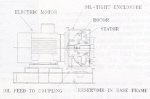
To limit the torque transmitted and thereby extend the start-up time of the conveyor, the solenoid
valve is closed for short periods of time thus momentarily reducing the coupling fill. Control of
the solenoid valve is effected by measuring motor power through a PLC.
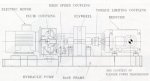
Fig. 11 shows the layout of each drive unit.
4.2 Belt Inspection
By setting a needle valve in the hydraulic circuit the oil fill can be markedly reduced, and the
coupling slip increased. This is employed to reduce the belt speed to about 1 m/s for belt inspection
purposes. From the elevated slip conditions, the heat gained by the oil is dissipated in an airblast
radiator fitted in series in the hydraulic circuit. Thus, separate pony drives are obviated.
4.3 Assessment of Electrical Variable Speed Drive
Early in the project, it was decided to investigate another drive system: an AC variable speed
drive. The choice of drive was a pulse width modulated (PWM), current-controlled inverter feeding
a squirrel cage motor. The same arrangement of the drive units on the primary and secondary
pulleys was used, but each motor would drive the same reducer directly.
AAC, requested the Department of Electrical Engineering of the University of the Witwatersrand (WITS)
to collaborate with simulation work. The complete drive system was simulated, including the supply,
the converter, the motor and the mechanical load. The conveyor model, developed by AAC, was used
as a sub-system of the WITS in-house package.
The work demonstrated that an AC variable speed drive was technically suited to drive the conveyor.
However, it was decided to continue with the fluid coupling option on the basis of cost, simplicity,
ease of trouble-shooting, and standardization with other drives.
5. Design Audit
A design audit was contracted to Bateman Materials Handling Limited, using the computer software as
developed by Conveyor Dynamics Incorporated of the USA. Work progressed, on a co-operative basis
with AAC, to refine the mechanical details.
The audit procedure consisted of undertaking a dynamic simulation of the starting and stopping
cycles of the conveyor, as statically designed by AAC, under various load conditions.
5.1 Shut-Down Analysis
Shut-down simulations (power outage) confirmed that the conveyor was subject to major tension
fluctuations, during stopping, which would adversely affect the ability of the belt to remain in
the troughing idlers in the horizontal curves. Braking or inertia devices were suggested. Further
simulations were undertaken to optimise the size of the chosen flywheel, with the aim of achieving
the smoothest possible shut-down profile on both the velocity and tension distributions. Figs. 12
and 13 show the resultant effect of the flywheel. Also, the flywheel has the effect of reducing
take-up movement from a predicted 4 m travel to 1.3 M.

Fig. 12: Velocity profiles on shut-down
Fig. 13: Tension profiles on shut-down
5.2 Start-Up Analysis
The procedure adopted for the start-up analysis followed the same format as the shut-down analysis.
Once the relevant performance curves were obtained from the fluid coupling supplier, the torque/time
parameters were incorporated into the model which allowed for the simulation of the start-up sequence.
This same procedure would apply to any soft-start system.
5.3 Aborted Start Analysis
To conclude the analysis, a series of "what-if" scenarios were undertaken, revolving around the
aborted start, i.e. the tripping of the drive motors when belt tensions were peaking during
start-up.
This work concluded that, even under extreme conditions, tension waves could not be generated which
would adversely affect the performance of the conveyor in the horizontal curves. This was as a
result of the damping effect of the flywheels.
5.4 Idler Banking in Horizontal Curves
Having obtained full tension profiles, at points along the length of the conveyor, from the starting
and stopping cycles of the conveyor, it was then possible to analyse the curve geometry and calculate
idler banking angles. The horizontal drift of the belt was determined, using a gravity principle,
throughout the tension profiles, for various idler banking angles.
Thus, by being able to predict the tensions at the horizontal curve tangent points, it was possible
to calculate the expected belt drift for various load conditions. Table 2 shows a typical
simulation output.
Type |
Load
% |
Tension
kN |
Bank
angle [°]
|
Radius
horiz.[m]
|
Radius
vert.[m]
|
Belt
drift[mm]
|
| Carry |
100 |
120 |
6 |
1350 |
1000 |
-3 |
| Carry |
50 |
80 |
6 |
1350 |
1000 |
-4 |
| Carry |
0 |
60 |
6 |
1350 |
1000 |
75 |
| Carry |
100 |
20 |
4 |
1330 |
500 |
-30 |
| Carry |
50 |
20 |
4 |
1330 |
500 |
-40 |
| Carry |
0 |
30 |
4 |
1330 |
500 |
-20 |
| Return |
0 |
40 |
2 |
1350 |
1000 |
50 |
| Return |
0 |
30 |
2 |
1330 |
500 |
25 |
Table 2: Expected belt drift in horizontal curves
From the above it can be seen that the expected belt displacement about its
centre-line will vary
between 75 mm inside the curve to 40 mm outside on the carry strand and between 25 and 50 mm inside
on the return strand.
5.5 Idler Rolling Resistance
The idler rolling resistance was considered to be critical for the successful operation of the system,
and continues to be so. There have been cases in the past, where long overland conveyors have
required every other carrying idler set to be removed during commissioning, in order to get the belt
to start initially. This process had to be repeated with alternating idler sets until they had been
run in. The cost and duration of such commissioning was completely unacceptable, and the idler
manufacturer was required to provide proof of the idler roll breakaway force. Values of a random sample
of idler rolls, both carry and return, were taken. The idler rolls were tested on a continuous
basis, in order to guarantee the results. A breakaway force of not more than 1.5 N was required.
The results of an analysis of a sample batch are shown in Table 3.
Pan
mass
[g]
|
Breakaway
force
[N]
|
Relative frequency (%)
|
return
|
carrying
|
50 |
0.5 |
4.9 |
3.1 |
100 |
1.0 |
58.5 |
56.3 |
150 |
1.5 |
24.4 |
37.5 |
200 |
2.0 |
12.2 |
3.1 |
Table 3: Analysis of sample batch
The spread of the breakaway force of the idler rolls tested is illustrated by the histogram in
Fig. 14.
Fig. 14: Idler roll breakaway force
The average values for the breakaway force were 1.20 N for the return idler rolls and
1.18 N for the carry idler rolls, both well within the limit of 1.5 N specified in the dynamic
analysis. Attention is being given to quantifying this aspect in the form of running resistance
values in a revision of the national standard, SABS 1313 [2], currently under review.
6. Construction and Commissioning
6.1 Overland Structure
In order to reduce capital expenditure, a source of used conveyor structure was found and the
sections designed into the overland portion of the conveyor. The structure was designed for a 1,050 m
wide conveyor and was equipped with a dog-house on open stringers without deckplates. The sections
are in 3.0 m lengths, with angle legs.
The use of second-hand structure required considerable preparation of the steelwork, though,
and all the steel was sand-blasted and painted on site. The elevated portions of the conveyor, at
the tail and at the head, were equipped with new steelwork, purpose-designed to cater for the belt
turnover and the elevation into the drive and transfer house. The overland conveyor stringer modules
were supported in augured holes filled with concrete after alignment for most of the overland section
of the conveyor. Elsewhere, the structure was supported on concrete sleepers where the ground was
undermined.
6.2 Tail Curve
A critical area was the tail curve, where the conveyor profile dipped under the road and rail
crossings. The tunnel was constructed in straight sections, each approximately 100 m long.
The construction was a simple rectangular culvert-type tunnel, with the soffit not quite 2.0 m above
the finished floor level. The conveyor steelwork was designed to be hung from the soffit, with the
vertical hangers welded to cast-in plates after alignment. The initial conveyor installation
followed the wall, thus there was no horizontal curve in that area, only three straight sections.
The belt did not bed down properly in the curve and a good deal of lateral drift was experienced at
first start-up, particularly in the tunnel area. The belt horizontal line consisted of a series of
interlinking curves of varying radius, some as low as 350 m, (the reason for the belt climb-out in
the tunnel). In addition, the design vertical curve into the tunnel was not followed, with the result
that the belt actually lifted out of the idlers in that area, with the accompanying uncontrolled
drift to the inner curve.
A survey was carried out in order to establish the correct conveyor set-out line in the tunnel.
When the structure was corrected, the belt performed well. The return idlers were spaced at 6.0 m
in the tunnel, instead of the design requirement of 3.0 m. The result was that lateral drift was
experienced in certain areas in the tunnel, with the belt drifting heavily into the structure on the
inner curve. The return idlers were banked in these areas, up to about 100 and more. However,
additional idlers were installed and the banking angle reduced to 4°.
6.3 Idler Banking
The idlers on both the carrying strand and return strand were adjusted along the full length of
both horizontal curves, in order to achieve the best lateral location of the belt under the varying
conditions. In a number of places in the curves, 'punches" were installed, over a distance of about 5
idler pitches, on the carrying strand only. The punch was a set of idlers where the banking was much
higher than normal. This has the effect of punching the belt back into line, should excessive drift
occur. The normal banking angles in the curves were 60 at the head end carrying strand, 40 at the
tail carrying strand and 2° for both the head and tail return strand curves. There were places
where the banking angle was increased by packing, to cater for inaccuracies in erection and
construction. There was a lead-in to each horizontal curve, over 10 idler pitches, where the
conventional carrying idlers were banked in steps to smooth the belt approach and depart sections in
the curve. After successful commissioning, the punches were removed and the belt allowed to settle
down normally.
7. Testing
After the completion of commissioning, tests were carried out to compare actual performance to
predicted performance. The test method was as follows.
7.1 Test Method
The conveyor was run through the cyclic phases of start-up, steady state and shut-down whilst being
loaded to 0% (empty), 70%, 100% (rated capacity) and 120% (20% overload).
During the steady state periods, manual readings were taken of:
- motor speed (rev/min)
- fluid coupling output speed (rev/min)
- motor voltage across each pair of phases
- motor current for each phase.
The time to start and stop was taken with a stopwatch, whilst monitoring the fluid coupling output
speed with a non-contact tachometer.
During the transient start-up and shut-down periods, recordings were made of the following
parameters:
- motor power (kW) for each motor
- belt speed (m/s) at the head and drive pulleys
- take-up displacement (m).
7.2 Results
Fig. 15 shows a typical motor power trace whilst starting a loaded belt. The initial gradual
increase of power delivered reaches a maximum when the upper power limit cuts the oil flow to the
coupling and the coupling fill diminishes. The lower power limit signals the oil to fill the
coupling again. The resultant saw-tooth profile continues until the entire belt is up to speed and
the absorbed power drops to normal operating levels.
Fig. 15: Motor power (start-up)
All three drive units shared the power requirement equally; typical steady state values were 92,
97 and 94 kW at 1 00% load. Manual reading confirmed the transducer readings. There was an average
3% slip over the fluid couplings at rated belt capacity (100% load).
7.3 Comparison with Design
The graphs (Figs. 16, 17 and 18) show the predicted plots for the loaded start showing anticipated
power draw, belt velocity at the drive pulley and take-up displacement, respectively. Superimposed
on these curves are the actual measured values.
Fig. 16: Comparison of motor power (start-up)
Fig. 17: Comparison of velocity (start-up)
Fig. 18: Comparison of take-up displacement (start-up)
It can be seen that both the motor power and belt velocity curves compare favorably. The predicted
curves wore obtained by re-running the simulation after lowering the friction factor from 0.022 to
0.017. This is consistent with the idler rolling resistance as discussed in section 5.5. Having
tested the rolls, it was discovered that the breakaway force was generally 1.0 - 1.2 N, which
is over 20% lower than the design factor of 1.5 N, resulting in a power saving of approximately
10%.
With regards to take-up displacement, as indicated in Fig. 18, a reasonable correlation can be seen
between the predicted and actual readings with regards to the expected travel path. However, the
theoretical analysis overstated the magnitude of travel, probably because of the conservative
estimation of belt modulus. The start-up and shut-down times for a loaded belt were 65 s and 44 s
respectively. Although the start-up time is less than the anticipated figure of 120 s, no dynamic
problems have been experienced. The lower start-up time was probably due to the reduced idler
rolling resistance coupled with the high power control levels selected in the PLC.
8. Award
The conveyor has been running successfully since being commissioned in October 1992. In the first
7 months of operation, 500,000 t of coal were conveyed to the RLT. This realised the intentions of
the project planners in transporting coal from the new Navigation Plant to the export terminal.
The conveyor system was recognised in August 1993 by receiving a 1993 Projects and Systems Award
from the South African Institution of Mechanical Engineers.
9. Conclusions
As part of the development of the new Landau Colliery, a 3.2 km overland conveyor, with tight
horizontal curves, was designed, commissioned and is running successfully.
The static design and dynamic simulations were carried out within the Anglo American Corporation
of South Africa Limited. Arising from the dynamic analysis, a number of changes were made to aspects
of the conveyor configuration to solve problems which arose.
Although a variable speed electrical drive was shown to be technically suited to the
conveyor, a fluid coupling was selected to control the belt start-up. Additional inertia, in the
form of drive flywheels, was added to extend and control the belt shut-down.
Acknowledgements
The authors wish to thank the Anglo American Corporation of South Africa Limited, and the Anglo
American Coal Corporation (Amcoal), for permission to publish this paper. The support of Mr. G.O.
PARNELL, Consulting Engineer of Amcoal, for this work is recognised.
The assistance of staff in both the AAC Mechanical Engineering and Electrical Engineering Departments
is gratefully acknowledged. Members of the WITS Department of Electrical Engineering contributed to
the assessment of the electrical variable speed drive. Bateman Materials Handling Limited assisted in
the auditing and commissioning of the conveyor. The staff of the Navigation Plant and the Rapid
Loading Terminal cooperated with commissioning and field testing. Surtees & Son (Pty) Ltd assisted in
carrying out some of the test runs with their measuring equipment.
The committee of the International Materials Handling Conference - Beltcon 7, has given permission
for this paper to be published in bulk solids handling.
References
- PAGE, J.L. and SHORTT, G.G.: Belt Conveyor Design Criteria within the
Anglo American Corporation; international Materials Handling Conference - Beltcon 6, 1991.
- SABS 1313: The Dimensions and Construction of Conveyor Belt Idlers and Rolls.
Appendix
Final Specification of Conveyor:
| Capacity |
design |
995 t/h |
Belt
|
Speed
width
belt class
construction
carcass
thickness
min. mass
service factor |
3,57 m/s
1050 mm
SABS 1366
ST 850 special
steelcord
4.18 mm
22,287 kg/m
6,637 |
Motor
|
type
power
frame size
speed |
squirrel cage
induction
3 x 160 kW
D 315 M
1485 rpm |
Fluid
Coupling |
type |
Voith 487 TPE |
Additional
Inertia
|
position
inertia |
input to each
reducer
40 kgm² each |
Reducer
|
type
ratio |
Flender FZG
B3SH9
26,556/1 |
Holdback
|
type
size
bore
minimum
L/S rating
location |
Falk
1105 NRT
180 mm
36 kNm
head pulley |
Take-up
|
type
total mass
T2 belt tension |
gravity
13,500 kg
30 kN |
| Pulleys |
face width |
1,100 mm |
Idlers
|
nominal
carrying pitch
carrying idlers
no. of rolls
impact idlers
transition
idlers
nominal
return pitch
return idlers
|
1200 mm
125 dia x 35° x
series 30
3
150 dia x 35° x
series 30
5°;12.5°;
20°;27.5°
6,000 mm
3,000 mm in
horiz curves
125 dia x 10° x
series 25
125 dia x flat x
series 25 |
| Nominal Idler |
| Banking in Horizontal Curves |
| |
carry:
Head curve |
6° |
| |
carry:
tail curve |
4° |
| |
return:
both curves |
2° |
Mr. J.L. Page, Mr. R.S. Hamilton and
Mr. G.G. Shortt
Anglo American Corporation of South Africa Ltd.,
P.O. Box 61587, Marshalltown 2107,
Republic of South Africa
Tel.: +27 11 638 91 11; Fax: +27 11 638 22 38
Mr. P. Staples
Conveyor Knowledge & Information Technology (Pty) Ltd.,
P.O. Box 1677, Bedfordview 2008,
Republic of South Africa
Tel.: +27 11 452 7347; Fax: +27 11 452 7386 |
|